Wed 14 May 2008
Generatingfunctorology
Posted by Edward Kmett under Haskell , Mathematics , Type Theory[12] Comments
Ok, I decided to take a step back from my flawed approach in the last post and play with the idea of power series of functors from a different perspective.
I dusted off my copy of Herbert Wilf's generatingfunctionology and switched goals to try to see some well known recursive functors or species as formal power series. It appears that we can pick a few things out about the generating functions of polynomial functors.
As an example:
Maybe x = 1 + x
Ok. We're done. Thank you very much. I'll be here all week. Try the veal...
For a more serious example, the formal power series for the list [x] is just a geometric series:
[x] = mu y . 1 + x y -- the mu here is a pleasant fiction, more below = 1 + x (1 + x (1 + x (...))) = 1 + x + x^2 + x^3 + ... = 1/(1-x)
Given the power series of a functor, its nth coefficient * n! tells you how many distinguishable ways its constructors can house n values. If we see that a list of n values can be permuted n! ways this has some interesting possibilities for linearizing the storage of some functors. The list case is boring, we can store a finite list of n elements by supplying the length of the array and an array of n elements, hence (among other reasons) the mu above.
Lets try decorated binary trees:
data Tree x = Leaf | Node (Tree x) x (Tree x) Tree x = mu y. 1 + x * y * y = 1 + x * (1 + x * (...)^2)^2 = 1 + x + 2x^2 + 5x^3 + 14x^4 + 42x^5 + ...
It turns out the coefficients of our generating function are the Catalan numbers, A000108, commonly denoted C(n), which happen to be well known for among other things, being the number of ways you can build a binary tree of n nodes.
This tells us we could store a tree by storing a number n of nodes it contains, an array of that many nodes, and an index 0 < = i < C(n) to tell you which particular tree you selected. Not that this is likely to be an incredibly time-efficient encoding, but you could then fmap over the tree by just fmapping over your array.
For a formal power series,
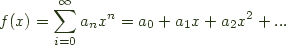
its derivative is given by differentiating the series term by term:
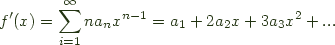
Consequently we can take the derivative of a list:
([]') x = 1 + 2x + 3x^2 + ... = 1/(1-x)^2 = ([] :*: []) x
and rederive the notion that a derivative/one hole context of a list can be represented by a pair of lists.
If we step slightly outside of the Haskell users' comfort zone and notion of a Functor and allow other Species, we get (as noted by apfelmus the other day) that Exp a is just a bag of elements with no predetermined order.
Exp x = 1 + x + x^2/2! + x^3/3! + ... = Bag x Since there are n! ways to order n elements and Bag manages to forget that information, we can get a feeling for the meaning of division in this setting. Similarly we can define: <pre lang="haskell"> Sinh x = x + x^3/3! + ... -- a Bag of some odd number of elements. Cosh x = 1 + x^2/2! + ... -- a Bag of some even number of elements.
Then by construction:
Exp = Cosh :+: Sinh
The derivative of Exp is Exp, of Cosh is Sinh, of Sinh is Cosh, all as you would expect.
We can handle other species as well:
Cycle a = 1 + x^2/2 + x^3/3 + x^4/4 + ... -- cycles Cycle_n a = x^n/n -- cycles of n elements Bag_n a = x^n/n! -- bags of n elements
That said, there seem to be some problems, not every functor is well behaved in this way. Lets take for instance the type of natural numbers given by the functor:
data Nat a = S (Nat a) | Z
Then the recurrence blows up, the coefficient for 0 is  !
!
Similarly, if we parameterized a functor on another value we have to deal with the number of cases that other value can denote.
Either a x = |a| + x (a,x) = |a| x
This is both good and bad, using the above, we can quickly establish an isomorphism between Either () and the Maybe Functor, but we blow up again for Either Integer. This gets even worse if we allow 'functors in space.' (i.e. functors that can contain functions)
On the other extreme, we might modify our tree example and remove the leaves, yielding infinite decorated cotrees.
Tree x = nu y. x * y * y
= x * (x * (...)^2)^2
= 0 + 0x + 0x^2 + 0x^3 + ...
Then a_n = 0 for all n in the natural numbers, so you can't use the coefficients of the generating function to tell you about the behavior of an infinite structure! It would appear that the generating function of a functor does not capture what happens in the greatest fixed point case, so we can only use generating functions to describe the behavior of data defined with mu, not in general codata defined by nu.
The Bags and Cycles above are nice examples, but if we wanted to rule out the non-polynomial Functors (from the Haskell perspective) in the above then we can simply limit ourselves to ordinary generating functions with natural number coefficients, that is to say generating functions of the form:
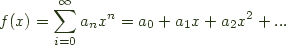
To choose to admit bags, cycles and other species etc. then you need merely also permit exponential generating functions with natural coefficients, that is to say, generating functions of the form:
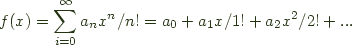

May 14th, 2008 at 3:35 pm
Flajolet and Sedgewick have a book called “Analytic Combinatorics” along these lines. It was available as a free pdf download for a while, but may actually be published at this point.
Your work on this is really interesting. I have, for years, had the damnedest time wrapping my head around generating functions. This presentation of Haskellisms as generating functions seems very interesting, and might be helpful in gaining an intuition in this area.
How would you model “evaluation” of your generating functions? I know how a Maybe monad behaves in the Haskell interpreter. Having defined it as you do, how do you combine it with other types and values? What does an expression look like, and what does reduction of one expression to a simpler express look like?
May 14th, 2008 at 3:53 pm
Well, a naive implementation for the ordinary generating function case is to just allocate an array of values the size of your structure, and store its size, and an ‘index’ into the possible structures of that size. This manipulates very poorly, but does allow for a linear time (heck, data parallel!) implementation of fmap. =)
A more practical implementation would necessarily want to take a generating function and generate a recurrence. This should give you a refolded version of the functor, like running the derivation for the list and tree functors backwards. This would let you do a transformation like turning the functor ‘Either Bool’ into a ternary constructor, which would then permit the use of partial-tagging to do dispatch with one case rather than two.
At this point though, I am still working on how to use these to model isomorphic structures, modeling contracts by division and subtraction, and what the right way is to extend it to cover codata.
Unfortunately, if we allow arbitrarily complex generating functions the comparison of the resulting streams requires an oracle for the halting problem, so, so far this is just a reasoning tool.
May 14th, 2008 at 6:24 pm
Edward,
Did you ever read this or this? I spent lots of time thinking similar thoughts but eventually got stuck.
May 15th, 2008 at 12:40 am
In fact, that is a fairly efficient representation for trees. I’ve used something very close to it before, in C.
You have to remember that C(n) is 4^n/n^1.5 times some constant. So to store a number between 0 and C(n), you need 2n – 1.5 log n bits.
If you think about that for a moment, it’s easy to do with exactly 2n bits: Introduce a parallel array of 2n bits, each element of which represents whether or not each node has a left or right child.
If you were compressing this bit vector, you could get closer to the asymptotic behaviour by noting that there’s some redundancy: In your array of 2n bits, exactly n-1 of them will be 1 and the remaining n+1 of them will be 0. It’s probably not hard to exploit this and recover a representation that’s optimal in an asymptotic sense.
May 15th, 2008 at 1:11 am
Ah, nice. My ‘naive encoding’ was apparently better than I thought =)
Currently mining the material written on species and what is in that Flajolet/Sedgewick book.
Awesome link, aed. Thanks!
May 16th, 2008 at 12:31 pm
Dan,
I love the notion of D as a singleton type.
I’ve been thinking about the idea of trying to represent the infinite cases using bivariate generating functions.
The idea would be that you ‘hang up on the number line’ quantities based on two parameters. One the number of traversals of the structure of size >= m that touch n values to give you an idea of the branching structure. Then clearly for n > m, the tail of the series = 0.
You then count the number of cases involved in using productive corecursion to visit n values in the structure rather than the number of distinct ways you can use well-founded recursion to build a structure of a given size.
I haven’t had time in the last couple of days to investigate the idea any further though.
[Edit: this doesn't appear to be sufficient and I haven't been able to find any good closed forms this way yet]
May 16th, 2008 at 2:14 pm
Hrmm. Just an observation:
If D^2 = 0, then given a functor F described by a generating function
F x = a_0 + a_1*x + a_2*x^2 + …
then
F D = a_0 + a_1*D
cuts off the series.
It also seems that D as a ’singleton pattern’ is affine (permits weakening), because nothing currently prevents you from ‘not using’ the D, as evidenced by the possibility of a_0 being non-zero.
May 16th, 2008 at 10:11 pm
Ah…it’s called affine logic. I don’t know the terminology.
May 16th, 2008 at 11:06 pm
Well, D is affine, as well as being singular in the fashion described.
Also, I think some of the usual isomorphisms such as the x^2 -> 2*x^2/2 one break down for the same reason the connection between ~~a and a breaks down, because we are working in an intuitionistic setting.
(At least my hand-wavy attempts to try to realize negative values as continuations accepting a given value type seemed to run into that)
May 17th, 2008 at 6:35 pm
Oh — I think I should stop seeing “+” as addition, and more as algabraic union — the possible values of Maybe x are 1 or x. So generating fuctions enumerate out the return values of a function (the “clothesline” upon which we hang numbers), but also can be composed together and manipulated with finite calculus and such.
Ach! So confusing.
May 28th, 2008 at 8:20 pm
aed: it’s common in category theory to use + for coproduct, which in the category of sets is indeed disjoint union. If you allow a natural number n to be represented by the finite set {1, 2, … n}, then + becomes ordinary addition :-)
November 27th, 2012 at 12:19 am
Đồ sơ sinh trọn gói…
[...]The Comonad.Reader » Generatingfunctorology[...]…