The Comonad.Reader

As you may recall, every functor in Haskell is strong, in the sense that if you provided an instance of Monad for that functor the following definition would satisfy the requirements mentioned here:

 
strength :: Functor f => a -> f b -> f (a,b)
strength = fmap . (,)
 

In an earlier post about the cofree comonad and the expression problem, I used a typeclass defining a form of duality that enables you to let two functors annihilate each other, letting one select the path whenever the other offered up multiple options. To have a shared set of conventions with the material in Zipping and Unzipping Functors, I have since remodeled that class slightly:

 
class Zap f g | f -> g, g -> f where
	zapWith :: (a -> b -> c) -> f a -> g b -> c
	zap :: f (a -> b) -> g a -> b
	zap = zapWith id
 

Interestingly, we can use the fact that every functor in Haskell is strong to derive not only one instance of Zap, but two, given any Adjunction .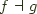

I'll give one instance here:

 
zapWithAdjunctionGF :: Adjunction g f =>
    (a -> b -> c) -> f a -> g b -> c
zapWithAdjunctionGF f a b =
    uncurry (flip f) . counit . fmap (uncurry (flip strength)) $
    strength a b
 

And I'll leave the substantially similar derivation of the following to the reader:

 
zapWithAdjunctionFG :: Adjunction f g => (a -> b -> c) -> f a -> g b -> c
 

Now, we would like to do the same thing we did with Representable last time, and just require the user of the Adjunction class to provide us with more instances, something like:

 
class (Zap f g, Zap g f, Representable g (f Void), Functor f) =>
    Adjunction f g | f -> g, g -> f where
        ...
 

But there is a problem: Adjunction composition.

If you will recall from before, we were able to define an instance for an Adjunction for a composition of two adjunctions:

 
newtype O f g a = Compose { decompose :: f (g a) }
 
instance (Functor f, Functor g) => Functor (f `O` g) where
        fmap f = Compose . fmap (fmap f) . decompose
 
instance (Adjunction f1 g1, Adjunction f2 g2) =>
    Adjunction (f2 `O` f1) (g1 `O` g2) where
        counit =
               counit .
               fmap (counit . fmap decompose) .
               decompose
        unit =
               Compose .
               fmap (fmap Compose . unit) .
               unit
 

The problem is that we have three different ways to build an instance of Zap for this composition and we would need to define two of them that conflict!

We would need both of these, which would lead to ambiguous instance heads:

 
instance (Adjunction f1 g1, Adjunction f2 g2) =>
    Zap (f2 `O` f1) (g1 `O` g2) where
        zapWith = zapWithAdjunctionFG
instance (Adjunction f1 g1, Adjunction f2 g2) =>
    Zap (g1 `O` g2) (f2 `O` f1) where
        zapWith = zapWithAdjunctionGF
 

Furthermore, we can also define a third instance of Zap over composition, which doesn't even care about Adjunction, which also conflicts with the above:

 
instance (Zap f g, Zap h k) => Zap (f `O` h) (g `O` k) where
    zapWith f a b =
        zapWith (zapWith f) (decompose a) (decompose b)
 

We could use the standard Haskell trick of making different compositions based on which instance of Zap you want to support, but the combinatorial explosion of constructors here when combined with the other reasons you may want to compose a pair of functors leads to a bit of absurdity, especially since I'm using it to capture a relationship no one cares about.

Consequently, category-extras does not capture this constraint.

Cozapping

As a final aside, we noted previously that Traversable functors were costrong. If a strong Adjunction gives rise to a couple of instances of Zap, we'd expect a similar relationship between a notion of Cozap and a costrong Adjunction.

But what would cozapping be?

First lets take a step back and break down zipWith into a couple of steps. If we note that zapWith (,) looks like:

 
prezapAdjunctionGF :: Adjunction g f => f a -> g b -> (a,b)
prezapAdjunctionGF a b =
    swap . counit . fmap (uncurry strength . swap) $ strength a b
    where swap ~(a,b) = (b,a)
 

Whereupon we can run the output through the canonical eval morphism for exponentials in :

 
eval :: (a -> b, a) -> b
eval (f,a) = f a
 

We can run everything backwards (modulo the noise caused by currying) in the first definition above and get:

 
precozapAdjunctionFG ::
    (Adjunction f g, Traversable f, Traversable g) =>
    Either a b -> Either (f a) (g b)
precozapAdjunctionFG =
    costrength . fmap (swap . costrength) . unit . swap
 

However, we lack a coeval morphism for coexponentials, since lacks coexponentials -- with good reason! If was a co-CCC then it would degenerate to a rather boring poset.

But that said, even getting this far, how many adjunctions are there between Traversable functors in Haskell, really?