The Comonad.Reader

I've had a few people ask me questions about Adjunctions since my recent post and a request for some more introductory material, so I figured I would take a couple of short posts to tie Adjunctions to some other concepts.

Representable Functors

A covariant functor 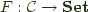is said to be representable by an object if it is naturally isomorphic to .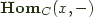

We can translate that into Haskell, letting play the role of with:

 
class Functor f => Representable f x where
    rep :: (x -> a) -> f a
    unrep :: f a -> (x -> a)
 
{-# RULES
"rep/unrep" rep . unrep = id
"unrep/rep" unrep . rep = id
 #-}
 

It is trivial to show that any two representations of a given functor must be isomorphic, and that there is a natural isomorphism between any two functors with the same representation, so we could strengthen the signature of the type class above by adding a pair of functional dependencies: f -> x, x -> f, but lets work without this straightjacket for now.

Example

We can represent the anonymous reader monad with its environment.

 
instance Representable ((->)x) x where
    rep = id
    unrep = id
 

Example

We could adopt the pleasant fiction that () has a single inhabitant to avoid bringing in an empty type, but lets do this correctly. Clearly the Identity functor needs no extra information from its representation.

 
data Void {- you'll need EmptyDataDecls -}
 
instance Representable Identity Void where
    rep f = Identity (f undefined)
    unrep = const . runIdentity
 

Adjunctions

If you recall the definition of Adjunctions over from before:

 
class (Functor f, Functor g) =>
    Adjunction f g | f -> g, g -> f where
        unit   :: a -> g (f a)
        counit :: f (g a) -> a
        leftAdjunct  :: (f a -> b) -> a -> g b
        rightAdjunct :: (a -> g b) -> f a -> b
 
        unit = leftAdjunct id
        counit = rightAdjunct id
        leftAdjunct f = fmap f . unit
        rightAdjunct f = counit . fmap f
 

We can generate a lot of representable functors, by turning to the theorem mentioned in the Wikipedia article about the representability of a right adjoint in terms of its left adjoint wrapped around a singleton element:

Any functor with a left adjoint is represented by (FX, ηX(•)) where X = {•} is a singleton set and η is the unit of the adjunction.

Well, earlier we defined a singleton set, Void, and can play the role of as we did above. For , we can translate the remainder quite easily:

 
repAdjunction :: Adjunction f g => (f Void -> a) -> g a
repAdjunction f = leftAdjunct f undefined
 
unrepAdjunction :: Adjunction f g => g a -> (f Void -> a)
unrepAdjunction = rightAdjunct . const
 

Now, as usual the way type class inference works in Haskell requires us to reason somewhat backwards.

You'd like to say:

 
instance Adjunction f g => Representable g (f Void) where
        rep = repAdjunction;
        unrep = unrepAdjunction
 

But if you do so, you can't define any other instances for Representable, you'll have used up the instance head, so the previous definitions couldn't be made.

On the other hand, you can create the obligation for an appropriate instance of Representable by changing the signature of Adjunction:

 
class (Representable g (f Void), Functor f) =>
    Adjunction f g | f -> g, g -> f where
        ...
 

Then the definitions for repAdjunction and unrepAdjunction can be used by any would-be Adjunction to automatically generate the corresponding Representable instance, just like liftM can alwyas be used to make a Haskell Monad into a Functor.

We can also go the other way and define an Adjunction given a representation for the right adjoint, but I'll leave that as an exercise for the reader. (Hint: you'll probably want to weaken the signature for Adjunction to remove the fundeps, so you can test some simple cases). You may also want to take a look at the section on Adjunctions as Kan extensions portion of the earlier post.

I have since modified category-extras definition of Adjunction to require the instance for Representable motivated above.

Haddock:
[Control.Functor.Adjunction]
[Control.Functor.Representable]