The Comonad.Reader

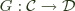Recently, a fellow in category land discovered a fact that we in Haskell land have actually known for a while (in addition to things most of us probably don't). Specifically, given two categories and , a functor , and provided some conditions in hold, there exists a monad , the codensity monad of .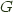

In category theory, the codensity monad is given by the rather frightening expression:

(more...)

Andrej Bauer recently gave a really nice talk on how you can exploit side-effects to make a faster version of Martin Escardo's pseudo-paradoxical combinators.

A video of his talk is available over on his blog, and his presentation is remarkably clear, and would serve as a good preamble to the code I'm going to present below.

Andrej gave a related invited talk back at MSFP 2008 in Iceland, and afterwards over lunch I cornered him (with Dan Piponi) and explained how you could use parametricity to close over the side-effects of monads (or arrows, etc) but I think that trick was lost in the chaos of the weekend, so I've chosen to resurrect it here, and improve it to handle some of his more recent performance enhancements, and show that you don't need side-effects to speed up the search after all!

(more...)

In the last few posts, I've been talking about how we can derive monads and monad transformers from comonads. Along the way we learned that there are more monads than comonads in Haskell.

The question I hope to answer this time, is whether or not we turn any Haskell Comonad into a comonad transformer.

(more...)

Last time in Monad Transformers from Comonads I showed that given any comonad we can derive the monad-transformer

 
newtype CoT w m a = CoT { runCoT :: w (a -> m r) -> m r
 

and so demonstrated that there are fewer comonads than monads in Haskell, because while every Comonad gives rise to a Monad transformer, there are Monads that do not like IO, ST s, and STM.

I want to elaborate a bit more on this topic.

(more...)

Last time, I showed that we can transform any Comonad in Haskell into a Monad in Haskell.

Today, I'll show that we can go one step further and derive a monad transformer from any comonad!

(more...)

Today I'll show that you can derive a Monad from any old Comonad you have lying around.

(more...)

Last time, I said that I was going to put our cheap new free monad to work, so let's give it a shot.

(more...)

Last time, I started exploring whether or not Codensity was necessary to improve the asymptotic performance of free monads.

This time I'll show that the answer is no; we can get by with something smaller.

(more...)

A couple of years back Janis Voigtländer wrote a nice paper on how one can use the codensity monad to improve the asymptotic complexity of algorithms using the free monads. He didn't use the name Codensity in the paper, but this is essentially the meaning of his type C.

I just returned from running a workshop on domain-specific languages at McMaster University with the more than able assistance of Wren Ng Thornton. Among the many topics covered, I spent a lot of time talking about how to use free monads to build up term languages for various DSLs with simple evaluators, and then made them efficient by using Codensity.

This has been shown to be a sufficient tool for this task, but is it necessary?

(more...)

Grant B. asked me to post the derivation for the right and left Kan extension formula used in previous Kan Extension posts (1,2). For that we can turn to the definition of Kan extensions in terms of ends, but first we need to take a couple of steps back to find a way to represent (co)ends in Haskell.

(more...)

I want to spend some more time talking about Kan extensions, composition of Kan extensions, and the relationship between a monad and the monad generated by a monad.

But first, I want to take a moment to recall adjunctions and show how they relate to some standard (co)monads, before tying them back to Kan extensions.

Adjunctions 101

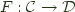An adjunction between categories and consists of a pair of functors , and 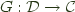and a natural isomorphism:

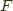We call the left adjoint functor, and the right adjoint functor and an adjoint pair, and write this relationship as

(more...)

I think I may spend a post or two talking about Kan extensions.

They appear to be black magic to Haskell programmers, but as Saunders Mac Lane said in Categories for the Working Mathematician:

All concepts are Kan extensions.

So what is a Kan extension? They come in two forms: right- and left- Kan extensions.

First I'll talk about right Kan extensions, since Haskell programmers have a better intuition for them.

(more...)