The Comonad.Reader

In the previous two posts, we've built up a whole range of applicatives, out of Const, Identity, Reader, Compose, Product, Sum, and Fix (and some higher-order analogues). Sum has given us the most trouble, but in some sense has been the most powerful, letting us write things like possibly eventually terminating lists, or trees, or in fact any sort of structure with branching alternatives. In this post, I want to think a bit more about why it is that Sum is the trickiest of the bunch, and more generally, what we can say about when two applicative structures are the "same". In the process of doing so, we'll invent something a lot like Traversable en passant.

Let's do some counting exercises. Product Identity Identity holds exactly two things. It is therefore isomorphic to ((->) Bool), or if we prefer, ((->) Either () ()). That is to say that a pair that holds two values of type a is the same as a function that takes a two-valued type and yields a value of type a. A product of more functors in turn is isomorphic to the reader of the sum of each of the datatypes that "represent" them. E.g. Product (Product Identity Identity) (Product (Const ()) Identity) is iso to ((->) (Either (Either () ()) ()), i.e. a data type with three possible inhabitants. In making this move we took Product to Either -- multiplication to sum. We can pull a similar trick with Compose. Compose (Product Identity Identity) (Product Identity Identity) goes to ((->) (Either () (),Either () ())). So again we took Product to a sum type, but now we took Compose to a pair -- a product type! The intuition is that composition multiplies the possibilities of spaces in each nested functor.

Hmm.. products go to sums, composition goes to multiplication, etc. This should remind us of something -- these rules are exactly the rules for working with exponentials. x^n * x^m = x^(n + m). (x^n)^m = x^(n*m). x^0 = 1, x^1 = x.

Seen from the right standpoint, this isn't surprising at all, but almost inevitable. The functors we're describing are known as "representable," a term which derives from category theory. (See appendix on representable functors below).

In Haskell-land, a "representable functor" is just any functor isomorphic to the reader functor ((->) a) for some appropriate a. Now if we think back to our algebraic representations of data types, we call the arrow type constructor an exponential. We can "count" a -> x as x^a, since e.g. there are 3^2 distinct functions that inhabit the type 2 -> 3. The intuition for this is that for each input we pick one of the possible results, so as the number of inputs goes up by one, the number of functions goes up by multiplying through by the set of possible results. 1 -> 3 = 3, 2 -> 3 = 3 * 3, (n + 1) -> 3 = 3 * (n -> 3).

Hence, if we "represent" our functors by exponentials, then we can work with them directly as exponentials as well, with all the usual rules. Edward Kmett has a library encoding representable functors in Haskell.

Meanwhile, Peter Hancock prefers to call such functors "Naperian" after John Napier, inventor of the logarithm (See also here). Why Naperian? Because if our functors are isomorphic to exponentials, then we can take their logs! And that brings us back to the initial discussion of type mathematics. We have some functor F, and claim that it is isomorphic to -^R for some concrete data type R. Well, this means that R is the logarithm of F. E.g. (R -> a, S -> a) =~ Either R S -> a, which is to say that if log F = R and log G =~ S, then log (F * G) = log F + log G. Similarly, for any other data type n, again with log F = R, we have n -> F a =~ n -> R -> a =~ (n * R) -> a, which is to say that log (F^n) =~ n * log F.

This gives us one intuition for why the sum functor is not generally representable -- it is very difficult to decompose log (F + G) into some simpler compound expression of logs.

So what functors are Representable? Anything that can be seen as a fixed shape with some index. Pairs, fixed-size vectors, fixed-size matrices, any nesting of fixed vectors and matricies. But also infinite structures of regular shape! However, not things whose shape can vary -- not lists, not sums. Trees of fixed depth or infinite binary trees therefore, but not trees of arbitrary depth or with ragged structure, etc.

Representable functors turn out to be extremely powerful tools. Once we know a functor is representable, we know exactly what its applicative instance must be, and that its applicative instance will be "zippy" -- i.e. acting pointwise across the structure. We also know that it has a monad instance! And, unfortunately, that this monad instance is typically fairly useless (in that it is also "zippy" -- i.e. the monad instance on a pair just acts on the two elements pointwise, without ever allowing anything in the first slot to affect anything in the second slot, etc.). But we know more than that. We know that a representable functor, by virtue of being a reader in disguise, cannot have effects that migrate outwards. So any two actions in a representable functor are commutative. And more than that, they are entirely independent.

This means that all representable functors are "distributive"! Given any functor f, and any data type r, then we have

 
distributeReader :: Functor f => f (r -> a) -> (r -> f a)
distributeReader fra = \r -> fmap ($r) fra
 

That is to say, given an arrow "inside" a functor, we can always pull the arrow out, and "distribute" application across the contents of the functor. A list of functions from Int -> Int becomes a single function from Int to a list of Int, etc. More generally, since all representable functors are isomorphic to reader, given g representable, and f any functor, then we have: distribute :: (Functor f, Representable g) => f (g a) -> g (f a).

This is pretty powerful sauce! And if f and g are both representable, then we get the transposition isomorphism, witnessed by flip! That's just the beginning of the good stuff. If we take functions and "unrepresent" them back to functors (i.e. take their logs), then we can do things like move from ((->) Bool) to pairs, etc. Since we're in a pervasively lazy language, we've just created a library for memoization! This is because we've gone from a function to a data structure we can index into, representing each possible argument to this function as a "slot" in the structure. And the laziness pays off because we only need to evaluate the contents of each slot on demand (otherwise we'd have a precomputed lookup table rather than a dynamically-evaluated memo table).

And now suppose we take our representable functor in the form s -> a and paired it with an "index" into that function, in the form of a concrete s. Then we'd be able to step that s forward or backwards and navigate around our structure of as. And this is precisely the Store Comonad! And this in turn gives a characterization of the lens laws.

What this all gives us a tiny taste of, in fact, is the tremendous power of the Yoneda lemma, which, in Haskell, is all about going between values and functions, and in fact captures the important universality and uniqueness properties that make working with representable functors tractable. A further tiny taste of Yoneda comes from a nice blog post by Conal Elliott on memoization.

Extra Credit on Sum Functors

There in fact is a log identity on sums. It goes like this:

log(a + c) = log a + log (1 + c/a)

Do you have a useful computational interpretation of this? I've got the inklings of one, but not much else.

Appendix: Notes on Representable Functors in Hask.

The way to think about this is to take some arbitrary category C, and some category that's basically Set (in our case, Hask. In fact, in our case, C is Hask too, and we're just talking about endofunctors on Hask). Now, we take some functor F : C -> Set, and some A which is an element of C. The set of morphisms originating at A (denoted by Hom(A,-)) constitutes a functor called the "hom functor." For any object X in C, we can "plug it in" to Hom(A,-), to then get the set of all arrows from A to X. And for any morphism X -> Y in C, we can derive a morphism from Hom(A,X) to Hom(A,Y), by composition. This is equivalent to, in Haskell-land, using a function f :: x -> y to send g :: a -> x to a -> y by writing "functionAToY = f . g".

So, for any A in C, we have a hom functor on C, which is C -> Set, where the elements of the resultant Set are homomorphisms in C. Now, we have this other arbitrary functor F, which is also C -> Set. Now, if there is an isomorphism of functors between F, and Hom(A,_), then we say F is "representable". A representable functor is thus one that can be worked with entirely as an appropriate hom-functor.

While the previous post in this series was relatively immediately applicable, this one has constructions I definitely wouldn't recommend in production code. However, they do take us further in exploring the universe of applicative functors, and, more broadly, exploring which data types provide which properties by construcion.

It's well known that if you have any Functor F a, you can take its "fixpoint", creating a structure of infinitely nested Fs, like so. F (F (F (...) ) ) Since we can't have infinite types directly in Haskell, we introduce the Fix newtype:

 
newtype Fix f = Fix (f (Fix f))

This "wraps up" the recursion so that GHC accepts the type. Fix f is a Fix constructor, containing an "f" of Fix f inside. Each in turn expands out, and soforth. Fixpoints of functors have fixedpoints of functors inside 'em. And so on, and so on, ad infinitum.

(Digression: We speak of "algebraic data types" in Haskell. The "algebra" in question is an "F-algebra", and we can build up structures with fixpoints of functors, taking those functors as initial or terminal objects and generating either initial algebras or terminal coalgebras. These latter two concepts coincide in Haskell in the Fix description given above, as greatest and least fixpoints of data types in Haskell turn out to be the same thing. For more background, one can go to Wadler's "Recursive Types for Free," or Jacobs and Rutten's "Tutorial on (Co)Algebras and (Co)Induction" for starters.)

The family of functors built from our friends Const, Sum, Product, and Reader (exponentiation) are known as Polynomial Functors. If we take closure of these with a proper fixpoint construct (that lets us build infinite structures), we get things that are variously known as Containers, Shapely Types, and Strictly Positive types.

One irritating thing is that the fixpoint of a functor as we've written it is no longer itself a functor. The type constructor Fix is of kind (* -> *) -> *, which says it takes an "f" which takes one argument (e.g. "Maybe" or "Identity" or etc.) and returns a proper type (i.e. a value at the type level of kind *).

We want a fixpoint construction that gives back something of kind * -> * — i.e. something that is a type constructor representing a functor, and not just a plain old type. The following does the trick.

 
newtype FixF f a = FixF (f (FixF f) a)
deriving instance (Show (f (FixF f) a)) => Show (FixF f a)

(I learned about FixF from a paper by Ralf Hinze, but I'm sure the origins go back much further).

FixF is of kind ((* -> *) -> * -> *) -> * -> *. It takes the fixpoint of a "second-order Functor" (a Functor that sends a Functor to another Functor, i.e. an endofunctor on the functor category of hask), to recover a standard "first order Functor" back out. This sounds scary, but it isn't once you load it up in ghci and start playing with it. In fact, we've encountered second order functors just recently. Product, Sum, and Compose are all of kind (* -> *) -> (* -> *) -> * -> *. So they all send two functors to a third functor. That means that Product Const, Sum Identity and Compose Maybe are all second-order functors, and things appropriate to take our "second-order fixpoint" of.

Conceptually, "Fix f" took a value with one hole, and we filled that hole with "Fix f" so there was no room for a type parameter. Now we've got an "f" with two holes, the first of which takes a functor, and the second of which is the hole of the resulting functor.

Unlike boring old "Fix", we can write Functor and Applicative instances for "FixF", and they're about as simple and compositional as we could possibly hope.

instance Functor (f (FixF f)) => Functor (FixF f) where
    fmap f (FixF x) = FixF $ fmap f x
 
instance Applicative (f (FixF f)) => Applicative (FixF f) where
    pure x = FixF $ pure x
    (FixF f) < *> (FixF x) = FixF (f < *> x)

But now we run into a new problem! It seems like this "a" parameter is just hanging out there, doing basically nothing. We take our classic functors and embed them in there, and they still only have "one hole" at the value level, so don't actually have any place to put the "a" type we now introduced. For example, we can write the following:

-- FixF . Compose . Just . FixF . Compose $ Nothing
-- > FixF (Compose (Just (FixF (Compose Nothing))))
-- :t FixF (Compose (Just (FixF (Compose Nothing))))
-- > FixF (Compose Maybe) a

We now introduce one new member of our basic constructions — a second order functor that acts like "const" on the type level, taking any functor and returning Identity.

 
newtype Embed (f :: * -> *) a = Embed a deriving (Show)
 
instance Functor (Embed f) where
    fmap f (Embed x) = Embed $ f x
 
instance Applicative (Embed f) where
    pure x = Embed x
    (Embed f) < *> (Embed x) = Embed (f x)

Now we can actually stick functorial values into our fixpoints:

-- FixF $ Embed "hi"
-- > FixF (Embed "hi")
 
-- fmap (++ " world") $ FixF (Embed "hi")
-- > FixF (Embed "hi world")
 
-- FixF . Product (Embed "hi") .
--        FixF . Product (Embed "there") . FixF $ undefined
-- > FixF (Product (Embed "hi")
--   (FixF (Product (Embed "there")
--   (FixF *** Exception: Prelude.undefined

You may have noticed that we seem to be able to use "product" to begin a chain of nested fixpoints, but we don't seem able to stick a "Maybe" in there to stop the chain. And it seems like we're not even "fixing" where we intend to be:

-- :t FixF . Product (Embed "hi") . FixF . Product (Embed "there") . FixF $ undefined
-- > FixF (Product (Embed f)) [Char]

That's because we're applying Product, takes and yields arguments of kind * -> * in a context where we really want to take and yield second-order functors as arguments — things of kind (* -> *) -> * -> *. If we had proper kind polymorphism, "Product" and "ProductF" would be able to collapse (and maybe, soon, they will). But at least in the ghc 7.4.1 that I'm working with, we have to write the same darn thing, but "up a kind".

data ProductF f g (b :: * -> *) a =
      ProductF (f b a) (g b a) deriving Show
 
instance (Functor (f b), Functor (g b)) =>
         Functor (ProductF f g b) where
                fmap f (ProductF x y) = ProductF (fmap f x) (fmap f y)
 
instance (Applicative (f b), Applicative (g b)) =>
         Applicative (ProductF f g b) where
               pure x = ProductF (pure x) (pure x)
              (ProductF f g) < *> (ProductF x y) = ProductF (f < *> x) (g < *> y)

We can now do the following properly.

yy = FixF . ProductF (Embed "foo") $ InL $ Const ()
xx = FixF . ProductF (Embed "bar") . InR .
        FixF . ProductF (Embed "baz") . InL $ Const ()

So we've recovered proper lists in Haskell, as the "second-order fixpoint" of polynomial functors. And the types look right too:

-- :t yy
-- > FixF (ProductF Embed (Sum (Const ()))) [Char]

Because we've built our Applicative instances compositionally, we have an applicative for our list list construction automatically:

-- (++) < $> yy < *> xx
-- > FixF (ProductF (Embed "foobar") (InL (Const ())))

This is precisely the "ZipList" applicative instance. In fact, our applicative instances from this "functor toolkit" are all "zippy" — matching up structure where possible, and "smashing it down" where not. This is because Sum, with its associated natural transformation logic, is the only way to introduce a disjoint choice of shape. Here are some simple examples with Sum to demonstrate:

-- liftA2 (++) (InL (Identity "hi")) $
--      InR (Product (Identity " there") (Const ([12::Int])))
-- > InL (Identity "hi there")
-- liftA2 (++) (InR (Identity "hi")) $ InL (Product (Identity " there") (Const ([12::Int])))
-- > InL (Product (Identity "hi there") (Const [12]))

We're always "smashing" towards the left. So in the first case, that means throwing away half of the pair. In the second case, it means injecting Const mempty into a pair, and then operating with that.

In any case, we now have infinite and possibly infinite branching structures. And not only are they Functors, but they're also Applicatives, and in a way that's uniform and straightforward to reason about.

In the next post, we'll stop building out our vocabulary of "base" Functors (though it's not quite complete) and instead push forward on what else these functors can provide "beyond" Applicative.

By and large, there are two sorts of proof systems that people use (these days) when studying logic: natural deduction, and sequent calculus. I know of at least one other---Hilbert style---but it is older, and the above systems were invented due to dissatisfaction with Hilbert systems (for a programming analogy, Hilbert systems are like programming entirely with combinators (S, K, etc.), rather than a lambda calculus).

Natural Deduction

Probably the best way to categorize the difference, for the purpose of where we're eventually going, is that natural deduction focuses on the ways to build proof terms up from their constituent parts. This comes in the form of introduction and elimination rules for the various propositions. For instance, the rules for conjunction are:

This spartan style gets a bit annoying (in my opinion) for the hypothetical premises of the implication introduction, but this can be solved by adding contexts:

This is the style most commonly adopted for presenting type theories, except we reason about terms with a type, rather than just propositions. The context we added for convenience above also becomes fairly essential for keeping track of variables:

As can be seen, all the rules involve taking terms from the premise and building on them in the conclusion.

Sequent Calculi

The other type of system in question, sequent calculus, looks very similar, but represents a subtle shift in focus for our purposes (sequent calculi are a lot more obviously different when presenting classical logics). First, the inference rules relate sequents, which look a lot like our contextual judgments above, and I'll write them the same way. The difference is that not all rules operate on the conclusion side; some operate just on the context. Generally, introduction rules stay similar to natural deduction (and are called right rules), while elimination rules are replaced by manipulations of the context, and are called left rules. For pairs, we can use the rules:

We could also have two separate left rules:

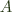But these two different sets are equivalent as long as we're not considering substructural logics. Do note, however, that we're moving from on the top left to 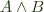on the bottom left, using the fact that is sufficient to imply . That is, projections apply contravariantly to the left.

It turns out that almost no type theory is done in this style; natural deduction is far and away more popular. There are, I think, a few reasons for this. The first is: how do we even extend the left rules to type theory (eliminations are obvious, by contrast)? I know of two ways. The first is to introduce pattern matching into the contexts, so our left rule becomes:

This is an acceptable choice (and may avoid some of the pitfalls in the next option), but it doesn't gel with your typical lambda calculus. It's probably more suited to a pattern calculus of some sort (although, even then, if you want to bend your brain, go look at the left rule for implication and try to figure out how it translates into such a theory; I think you probably need higher-order contexts of some sort). Anyhow, I'm not going to explore this further.

The other option (and one that I've seen in the literature) is that left rules actually involve a variable substitution. So we come up with the following rule:

And with this rule, it becomes (I think) more obvious why natural deduction is preferred over sequent calculus, as implementing this rule in a type checker seems significantly harder. Checking the rules of natural deduction involves examining some outer-most structure of the term, and then checking the constituents of the term, possibly in an augmented context, and which rule we're dealing with is always syntax directed. But this left rule has no syntactic correspondent, so it seems as though we must nondeterministically try all left rules at each step, which is unlikely to result in a good algorithm. This is the same kind of problem that plagues extensional type theory, and ultimately results in only derivations being checkable, not terms.

The Type Class Connection

However, there are certain problems that I believe are well modeled by such a sequent calculus, and one of them is type class checking and associated dictionary translations. This is due mainly to the fact that the process is mainly context-directed term building, rather than term-directed type checking. As far as the type class algorithm goes, there are two interesting cases, having to do with the following two varieties of declaration:

 
  class Eq a => Ord a where ...
  instance (Eq a, Eq b) => Eq (a, b) where ...
 

It turns out that each of these leads to a left rule in a kind of type class sequent calculus:

That is:

1. if Eq a is a sufficient constraint for M : T, then the stronger constraint Ord a is also sufficient, so we can discharge the Eq a constraint and use Ord a instead.
2. We can discharge an Eq (a, b) constraint using two constraints, Eq a, Eq b together with an instance telling us how to do so. This also works for instances without contexts, giving us rules like:

   

Importantly, the type inference algorithm for type classes specifies when we should use these rules based only on the contexts we're dealing with. Now, these look more like the logical sequent rules, but it turns out that they have corresponding type theory-like versions when we consider dictionary passing:

And this kind of substituting into dictionary variables produces exactly the evidence passing translation we want.

Another way to look at the difference in feasibility is that type checking involves moving bottom-to-top across the rules; in natural deduction, this is always easy, and we need look only at the terms to figure out which we should do. Type class checking and dictionary translation moves from top-to-bottom, directed by the left hand context, and produces terms on the right via complex operations, and that is a perfect fit for the sequent calculus rules.

I believe this corresponds to the general opinion on those who have studied sequent calculi with regard to type theory. A quick search revealed mostly papers on proof search, rather than type checking, and type classes rather fall into that realm (they're a very limited form of proof search).

Last time we derived an entailment relation for constraints, now let's get some use out of it.

Reflecting Classes and Instances

Most of the implications we use on a day to day basis come from our class and instance declarations, but last time we only really dealt with constraint products.

(more...)

Max Bolingbroke has done a wonderful job on adding Constraint kinds to GHC.

Constraint Kinds adds a new kind Constraint, such that Eq :: * -> Constraint, Monad :: (* -> *) -> Constraint, but since it is a kind, we can make type families for constraints, and even parameterize constraints on constraints.

So, let's play with them and see what we can come up with!

(more...)

Last time, I showed that we can build a small parsec clone with packrat support.

This time I intend to implement packrat directly on top of Parsec 3.

One of the main topics of discussion when it comes to packrat parsing since Bryan Ford's initial release of Pappy has been the fact that in general you shouldn't use packrat to memoize every rule, and that instead you should apply Amdahl's law to look for the cases where the lookup time is paid back in terms of repetitive evaluation, computation time and the hit rate. This is great news for us, since, we only want to memoize a handful of expensive combinators.

(more...)

You never heard of the Millenium Falcon? It's the ship that made the Kessel Run in 12 parsecs.

I've been working on a parser combinator library called trifecta, and so I decided I'd share some thoughts on parsing.

Packrat parsing (as provided by frisby, pappy, rats! and the Scala parsing combinators) and more traditional recursive descent parsers (like Parsec) are often held up as somehow different.

Today I'll show that you can add monadic parsing to a packrat parser, sacrificing asymptotic guarantees in exchange for the convenient context sensitivity, and conversely how you can easily add packrat parsing to a traditional monadic parser combinator library.

(more...)

Last night, Chung-Chieh Shan posted an example of a pointed-set monad on his blog, which happens to be isomorphic to a non-empty stream monad with a different emphasis.

But, I thought I should point out that the pointed set that he posted also has a comonadic structure, which may be exploited since it is just a variation on the "zipper comonad," a structure that is perhaps more correctly called a "pointing comonad."

(more...)

To those that have asked, I'm still alive.

I had to restore the blog database from a backup and so I lost a few posts, including the index for the various recursion schemes entries. Fortunately, before that happened I had replicated the catamorphism post as a knol.

Should I find myself with a copious glut of free time, I shall happily re-scribe and finish the rest, but I've been very busy.

Does anyone know of any work on "forgetful laziness?"

(more...)

Back in the days of HYLO, it was common to write hylomorphisms with an additional natural transformation in them. Well, I was still coding in evil imperative languages back then, but I have it on reliable, er.. well supposition, that this is probably the case, or at least that they liked to do it back in the HYLO papers anyways.

Transcoding the category theory mumbo-jumbo into Haskell, so I can have a larger audience, we get the following 'frat combinator' -- you can blame Jules Bean from #haskell for that.

 
hyloEta :: Functor f =>
     (g b -> b) ->
     (forall a. f a -> g a) ->
     (a -> f a)
hyloEta phi eta psi = phi . eta . fmap (hyloEta phi eta psi) . psi
 

We placed eta in the middle of the argument list because it is evocative of the fact that it occurs between phi and psi, and because that seems to be where everyone else puts it.

Now, clearly, we could roll eta into phi and get the more traditional hylo where f = g. Less obviously we could roll it into psi because it is a natural transformation and so the following diagram commutes:

This 'Hylo Shift' property (mentioned in that same paper) allows us to move the 'eta' term into the phi term or into the psi term as we see fit. Since we can move the eta term around and it adds no value to the combinator, it quietly returned to the void from whence it came. hyloEta offers us no more power than hylo, so out it goes.

So, if its dead, why talk about it?

(more...)

Wordpress changed the slug of this post, but Planet Haskell has the old link.

Here is the actual content.

Updated my little type-level 2s and 16s complement integer library to be ghc 6.6 friendly and uploaded it to hackage based on popular (er.. ok, well, singular) demand.

O.K. it was more of a polite request, but I did update it.