Mon 26 May 2008
Kan Extensions III: As Ends and Coends
Posted by Edward Kmett under Category Theory , Haskell , Kan Extensions , Mathematics[14] Comments
Grant B. asked me to post the derivation for the right and left Kan extension formula used in previous Kan Extension posts (1,2). For that we can turn to the definition of Kan extensions in terms of ends, but first we need to take a couple of steps back to find a way to represent (co)ends in Haskell.
Dinatural Transformations
Rather than repeat the definition here, we'll just note we can define a dinatural transformation in Haskell letting polymorphism represent the family of morphisms.
type Dinatural f g = forall a. f a a -> g a a
Ends
So what is an end?
An end is a universal dinatural transformation from some object e to some functor s.
Diving into the formal definition:
Given a functor  , and end of
, and end of 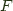 is a pair
is a pair 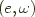 where
where  is an object of
is an object of  and omega is a dinatural transformation from e to S such that given any other dinatural transformation
and omega is a dinatural transformation from e to S such that given any other dinatural transformation 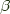 to S from another object x in
to S from another object x in  , there exists a unique morphism
, there exists a unique morphism 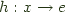 , such that
, such that 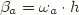 for every
for every  in
in  .
.
We usually choose to write ends as  , and abuse terminology calling
, and abuse terminology calling  the end of
the end of 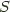 .
.
Note this uses a dinatural transformation from an object  in
in  , which we can choose to represent an arbitrary dinatural transformation from an object
, which we can choose to represent an arbitrary dinatural transformation from an object  to a functor
to a functor 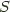 in terms of a dinatural transformation from the constant bifunctor:
in terms of a dinatural transformation from the constant bifunctor:
newtype Const x a b = Const { runConst :: x }
This leaves us with the definition of a dinatural transformation from an object as:
Dinatural (Const x) s ~ forall a. Const x a a -> s a a
but the universal quantification over the Const term is rather useless and the Const bifunctor is supplying no information so we can just specialize that down to:
type DinaturalFromObject x s = x -> forall a. s a a
Now, clearly for any such transformation, we could rewrite it trivially using the definition:
type End s = forall a. s a a
with 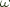 = id.
= id.
type DinaturalFromObject x s = x -> End s
And so End above fully complies with the definition for an end, and we just say e = End s abusing the terminology as earlier. The function 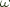 = id is implicit.
= id is implicit.
For End to be a proper end, we assume that s is contravariant in its first argument and covariant in its second argument.
Example: Hom
A good example of this is (->) in Haskell, which is as category theory types would call it the Hom functor for Hask. Then End (->) = forall a. a -> a which has just one inhabitant id if you discard cheating inhabitants involving fix or undefined.
We write 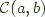 or
or 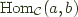 to denote
to denote a -> b. Similarly we use 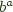 to denote an exponential object within a category, and since in Haskell we have first class functions using the same syntax this also translates to
to denote an exponential object within a category, and since in Haskell we have first class functions using the same syntax this also translates to a -> b. We'll need these later.
Example: Natural Transformations
If we define:
newtype HomFG f g a b = HomFG { runHomFG :: f a -> g b }
then we could of course choose to define natural transformations in terms of End as:
type Nat f g = End (HomFG f g) -- forall a. f a -> g a
Right Kan Extension as an End
Turning to Wikipedia or Categories for the Working Mathematician you can find the following definition for right Kan extension of 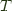 along
along 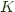 in terms of ends.
in terms of ends.

Working by rote, we note that 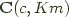 is just
is just c -> K m as noted above, and that 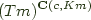 is then just
is then just (c -> K m) -> T m'. So now we just have to take the end over that, and read off:
newtype RanT k t c m m' = (c -> k m) -> t m' type Ran k t c = End (RanT k t c)
Which, modulo newtype noise is the same as the type previously supplied type:
newtype Ran f g c = Ran { runRan :: forall m. (c -> f m) -> g m }
Coends
The derivation for the left Kan extension follows similarly from defining coends over Hask in terms of existential quantification and copowers as products.
The coend derivation is complicated slightly by Haskell's semantics. Disposing of the constant bifunctor as before we get:
type DinaturalToObject s c = forall a. (s a a -> c)
Which since we want to be able to box up the s a a term separately, we need to use existential quantification.
(forall a. s a a -> c) ~ (exists a. s a a) -> c
We cannot represent this directly in terms of a type annotation in Haskell, but we can do so with a data type:
data Coend f = forall a. Coend (f a a)
Recall that in Haskell, existential quantification is represented by using universal quantification outside of the type constructor.
The main difference is that in our coend 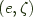 the function
the function 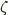 is now
is now runCoend instead of id, because we have a Coend data constructor around the existential. Technicalities make it a little more complicated than that even, because you can't define a well-typed runCoend and have to use pattern matching on the Coend data constructor to avoid having an existentially quantified type escape the current scope, but the idea is the same.
Left Kan Extension as a Coend
Then given the definition for the left Kan extension of 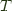 along
along 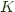 as a coend:
as a coend:

we can read off:
data LanT k t c m m' = LanT (k m -> c) (t m') type Lan k t c = Coend (LanT k t c)
Which is almost isomorphic to the previously supplied type:
data Lan k t c = forall m. Lan (k m -> c) (t m)
except for the fact that we had to use two layers of data declarations when using the separate Coend data type, so we introduced an extra place for a  to hide.
to hide.
A newtype isn't allowed to use existential quantification in Haskell, so this form forces a spurious case analysis that we'd prefer to do without. This motivates why category-extras uses a separate definition for Lan rather than the more elaborate definition in terms of Coend.
[Edit: Fixed a typo in the definition of RanT]

May 27th, 2008 at 5:27 am
Awesome! This helped my understanding a lot, thanks.
May 27th, 2008 at 3:45 pm
Hey! Stop writing posts faster than I can read them :-)
June 13th, 2008 at 5:41 pm
I’m curious as to how you would motivate Kan extensions as a functional programming (specifically Haskell) tool. The right Kan extension almost looks like the CPS-transform of “a”, except with variant answer types. Shan’s thesis on page 73 shows how the ordinary function type is modified via the presence of delimited control into something like a right Kan extension.
Care to shed some light on this (and its dual)?
June 14th, 2008 at 8:16 am
Well, you can look at the Codensity monad (Ran m m) of a monad m as a weaker form of ContT which isn’t allowed to use the type of the ultimate return value to ‘pull any tricks’. Consequently, it has fewer inhabitants than ContT and we can say more about them. My favorite example so far is in:
http://wwwtcs.inf.tu-dresden.de/~voigt/mpc08.pdf
That paper shows that you can substitute a reference to the Codensity monad of a free monad in many places where you’d use the original free monad and change the asymptotic performance of the resulting algorithm because the continuation ‘linearizes’ the cost of repeatedly traversing the tree by piling the cost up in the continuation so you only traverse once.
I’d conjecture that the left Kan extension of a cofree comonad should let us pile up the cost of mapping or extending cofree comonads similarly. Though here I have yet to actually generate any performance results here due to other distractions.
We _can_ however definitely do the same thing with the Yoneda and Coyoneda lemmas. The resulting (co)monads fit very closely to the operational characteristics of the base monad.
If you transform a monad with Yoneda you get a monad that has the same overall costs for return and >>=, but where if your monad had a non constant cost for map (such as in the free monad of anything other than the trivial functor that maps everything to _|_), you can fuse the costs of all of your maps together by accumulating them and applying them all at once during the next (>>=) (or when you extract f from the Yoneda f).
Similarly CoYoneda accumulates maps for comonads, which is a win if map is expensive (such as in the cofree comonad case).
You can get a feel for why this works by looking at:
http://comonad.com/haskell/category-extras/src/Control/Functor/Yoneda.hs
and noting what fmap does and how >>= works for Yoneda. and how fmap and extend work for CoYoneda.
In category-extras I have generalized all of the constructive algorithmic morphisms that use the free monad or cofree comonad (histomorphisms, futumorphisms, dynamorphisms, chronomorphisms) to support the codensity monad of the free monad, density comonad of the cofree comonad, Yoneda of the free monad, Coyoneda of the cofree comonad, etc by defining a couple of extra typeclasses that express their ‘Free-Like’ behavior in the spirit of the above linked paper by Voigtlaender in
http://comonad.com/haskell/category-extras/src/Control/Monad/Free.hs
The generalization can be seen in use here:
http://comonad.com/haskell/category-extras/src/Control/Morphism/Futu.hs
and the instances for Codensity here:
http://comonad.com/haskell/category-extras/src/Control/Monad/Codensity.hs
February 25th, 2009 at 7:45 pm
Now that I’ve been thinking about these things I can point out a tiny tiny typo:
data LanT k t c m m’ = LanT (k m -> c) (t m)
should probably be
data LanT k t c m m’ = LanT (k m -> c) (t m’)
though it makes no difference in the definition of Lan.
On a less trivial level, I still don’t know what theorem I could quote to justify that, say,
type DinaturalFromObject x s = x -> forall a. s a a
defines dinaturals from a constant functor. For a specific choice of s dinaturality is a free theorem. But how do you uniformly prove this for all s, implemented in Haskell, with the right c/contravariance in the arguments?
February 25th, 2009 at 9:02 pm
Hey Dan,
Fixed the LanT definition. (Woops!)
Re the dinatural transformation piece, I’m not as deep as I used to be in this area, so I’ll go back and see what I can dig up from whatever notes I still have from when I wrote this. I recall it seeming quite obvious at the time, but now I can only barely remember what dinaturality is. :) I’d be quite surprised (and pleased) if you came up with a counterexample, however. ;)
February 26th, 2009 at 12:29 am
All of the various types of naturality (including dinaturality and extranaturality) seem to arise as free theorems but I’ve not seen a paper spelling this out clearly – at least not in a form I’d recognise. I can’t tell if it’s because nobody has figured it the details, or if the papers are just over my head.
October 17th, 2009 at 11:15 pm
Just a minor typo note:
> newtype RanT f g c m m’ = (c -> K m) -> T m’
Should be:
> newtype RanT k t c m m’ = (c -> k m) -> t m’
right?
October 18th, 2009 at 4:35 pm
Wren: Fixed!
September 9th, 2010 at 1:44 am
Have you ever considered about contributing on additional web sites? You have some great content right here and I’m certain you can share a lot far more when you wrote some content throughout other web sites. You will discover a great deal of associated web-sites to check out. Only one thing to look at. I’m glad I know about it at least.
September 10th, 2010 at 12:28 pm
I have written bits and pieces here and there over the years — I used to write a lot of magazine articles in particular, and I think there is an old column by me still floating around on flipcode.
These days I have a lot less time for writing, however. What makes it to this blog are mostly just the things that I found interesting enough to share. To get the message out I largely rely on syndication through planet haskell and reddit, both of which makes the location of the source content less of an issue these days than it used to be. Those have more overlap with would-be readership for this sort of content than almost any mainstream web site I can know of.
June 24th, 2011 at 3:43 am
[...] I have spoken about this type (and another that will arise in a subsequent post) on this blog previously, in a series of posts on Kan Extensions. [ 1, 2, 3] [...]
July 7th, 2011 at 6:44 pm
Isn’t the type (exists a. f a a) the coproduct rather than the coend? The coend is the coproduct modulo the relation imposed by the commuting square (degenerate hexagon) in the definition of a dinatural transformation.
September 22nd, 2012 at 10:43 pm
[...] the integral notation denotes an end, and the square brackets denote a power, which allows us to take what is essentially an exponential [...]