Mon 1 Apr 2013
Japanese “ekmett” Workshop (Part 1 of 2)
Posted by Edward Kmett under Japan , Lenses , MathematicsNo Comments
A couple of weeks back one of my coworkers brought to my attention a several hour long workshop in Japan to go over and describe a number of my libraries, hosted by TANAKA Hideyuki — not the voice actor, I checked!
I was incredibly honored and I figured that if that many people (they had 30 or so registered attendees and 10 presentations) were going to spend that much time going over software that I had written, I should at least offer to show up!
I'd like to apologize for any errors in the romanization of people's names or misunderstandings I may have in the following text. My grasp of Japanese is very poor! Please feel free to send me corrections or additions!
Surprise!
Sadly, my boss's immediate reaction to hearing that there was a workshop in Japan about my work was to quip that "You're saying you're huge in Japan?" With him conspicuously not offering to fly me out here, I had to settle for surprising the organizers and attending via Google Hangout.
Commentary and Logs
@nushio was very helpful in getting me connected, and while the speakers gave their talks I sat on the irc.freenode.net #haskell-lens channel and Google Hangout and answered questions and provided a running commentary with more details and references. Per freenode policy the fact that we were logging the channel was announced -- well, at least before things got too far underway.
Here is the IRC session log as a gist. IKEGAMI Daisuke @ikegami__ (ikeg in the IRC log) tried to keep up a high-level running commentary about what was happening in the video to the log, which may be helpful if you are trying to follow along through each retroactively.
Other background chatter and material is strewn across twitter under the #ekmett_conf hash tag and on a japanese twitter aggregator named togetter

 and
and  , a functor
, a functor 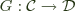 , and provided some conditions in
, and provided some conditions in  , the codensity monad of
, the codensity monad of 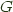 .
.![$ T^G(a) = \int_r \left[\mathcal{D}(a, Gr), Gr\right] $ $ T^G(a) = \int_r \left[\mathcal{D}(a, Gr), Gr\right] $](../../../latex/050bb5034bed82159df4c52c89c07f3c.png)