The Comonad.Reader

A couple of years back Janis Voigtländer wrote a nice paper on how one can use the codensity monad to improve the asymptotic complexity of algorithms using the free monads. He didn't use the name Codensity in the paper, but this is essentially the meaning of his type C.

I just returned from running a workshop on domain-specific languages at McMaster University with the more than able assistance of Wren Ng Thornton. Among the many topics covered, I spent a lot of time talking about how to use free monads to build up term languages for various DSLs with simple evaluators, and then made them efficient by using Codensity.

This has been shown to be a sufficient tool for this task, but is it necessary?

(more...)

A couple of days ago, I gave a talk at Boston Haskell about a shiny new speculative evaluation library, speculation on hackage, that I have implemented in Haskell. The implementation is based on the material presented as "Safe Programmable Speculative Parallelism" by Prakash Prabhu, G Ramalingam, and Kapil Vaswani at last month's PLDI.

I've uploaded a copy of my slides here:

* Introducing Speculation [PowerPoint | PDF]

(more...)

I've put together a poll about when folks would like to have the next meeting, if you're going to be in the area, please help us pick a date and time that works for you!

http://www.doodle.com/ux8mqaa9h2tngf6k

(more...)

I'm going to be out at Hac φ over the weekend cobbling together random bits and pieces of code, if you're going to be in the Philadelphia area, look us up!

In particular, I plan to spend my time working on my automatic differentiation library adding different directional traversals, and trying to combine them into a coherent framework.

I've uploaded a package named heaps to Hackage that provides Brodal-Okasaki bootstrapped skew-binomial heaps in Haskell.
(more...)

I've uploaded a package named rad to Hackage for handling reverse-mode automatic differentiation in Haskell.
(more...)

I gave a talk last night at Boston Haskell on finger trees.

In particular I spent a lot of time focusing on how to derive the construction of Hinze and Paterson's 2-3 finger trees via an extended detour into a whole menagerie of tree types, and less on particular applications of the final resulting structure.

(more...)

I'll be giving a talk tomorrow, Wednesday, September 16th, 2009 at the Boston Haskell User Group in the MIT CSAIL Reading Room (on the 8th floor of the William H. Gates tower of the Stata center) about mixing Oleg's iteratees with parsec and monoids to build practical parallel parsers and to cheaply reparse after local modifications are made to source code.

Ravi is trying to organize some time before hand during which people can get together and work on Haskell projects, or spend some time learning Haskell, so its not all scary academic stuff.

The meeting is scheduled from 7-9pm, and an ever growing number of us have been wandering down to the Cambridge Brewing Company afterwards to hang out and talk.

If you are curious about Haskell, or even an expert, or just happen to be interested in parallel programming and find yourself in the area, come on by.

I was asked to give two talks at the Boston Area Haskell User Group for this past Tuesday. The first was pitched at a more introductory level and the second was to go deeper into what I have been using monoids for lately.

The first talk covers an introduction to the mathematical notion of a monoid, introduces some of the features of my Haskell monoids library on hackage, and starts to motivate the use of monoidal parallel/incremental parsing, and the modification use of compression algorithms to recycle monoidal results.

The second talk covers a way to generate a locally-context sensitive parallel/incremental parser by modifying Iteratees to enable them to drive a Parsec 3 lexer, and then wrapping that in a monoid based on error productions in the grammar before recycling these techniques at a higher level to deal with parsing seemingly stateful structures, such as Haskell layout.

1. Introduction To Monoids (PDF)
2. Iteratees, Parsec and Monoids: A Parsing Trifecta (PDF)

Due to a late start, I was unable to give the second talk. However, I did give a quick run through to a few die-hards who stayed late and came to the Cambridge Brewing Company afterwards. As I promised some people that I would post the slides after the talk, here they are.

The current plan is to possibly give the second talk in full at either the September or October Boston Haskell User Group sessions, depending on scheduling and availability.

[ Iteratee.hs ]

I have updated the reflection package on hackage to use an idea for avoiding dummy arguments posted to the Haskell cafe mailing list by Bertram Felgenhauer, which adapts nicely to the case of handling Reflection. The reflection package implements the ideas from the Functional Pearl: Implicit Configurations paper by Oleg Kiselyov and Chung-chieh Shan.

Now, you no longer need to use big scary undefineds throughout your code and can instead program with implicit configurations more naturally, using Applicative and Monad sugar.

(more...)

Some people have requested my slides from the short talk I gave about monoids and monoidal parsing at Hac Phi. So, here they are.

• Hac Phi Slides (Powerpoint 2007)
• Hac Phi Slides (PDF)

There will be more to come at the next Boston Haskell User Group in August, where it looks like I'll be giving two short talks covering monoids. I may use the monoidal parsing engine from Kata as an example for the advanced talk if I have time and will start to cover parsing larger classes of grammars in general (regular languages, CFGs/TIGs, TAGs, PEGs, LALR, attribute-grammars, etc.)

About a year back I posted a field guide of recursion schemes on this blog and then lost it a few months later when I lost a couple of months of blog entries to a crash. I recently recovered the table of recursion schemes from the original post thanks to Google Reader's long memory and the help of Jeff Cutsinger.

The following recursion schemes can be found in category-extras, along with variations on the underlying themes, so this should work as a punch-list.

* This gives rise to a family of related recursion schemes, modeled in category-extras with distributive law combinators
† The scheme can be generalized to accept one or more F-distributive (co)monads.

Recently, Sean Leather took up the idea of incremental folds. [1] [2]. At the end of his first article on the topic he made a comment on how this was a useful design pattern and sagely noted the advice of Jeremy Gibbons that design patterns are more effective as programs, while complaining of cut and paste coding issues.

The following attempts to address these concerns.

(more...)

Last night, Chung-Chieh Shan posted an example of a pointed-set monad on his blog, which happens to be isomorphic to a non-empty stream monad with a different emphasis.

But, I thought I should point out that the pointed set that he posted also has a comonadic structure, which may be exploited since it is just a variation on the "zipper comonad," a structure that is perhaps more correctly called a "pointing comonad."

(more...)

As you may recall, every functor in Haskell is strong, in the sense that if you provided an instance of Monad for that functor the following definition would satisfy the requirements mentioned here:

 
strength :: Functor f => a -> f b -> f (a,b)
strength = fmap . (,)
 

In an earlier post about the cofree comonad and the expression problem, I used a typeclass defining a form of duality that enables you to let two functors annihilate each other, letting one select the path whenever the other offered up multiple options. To have a shared set of conventions with the material in Zipping and Unzipping Functors, I have since remodeled that class slightly:

(more...)

I've had a few people ask me questions about Adjunctions since my recent post and a request for some more introductory material, so I figured I would take a couple of short posts to tie Adjunctions to some other concepts.

Representable Functors

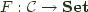A covariant functor is said to be representable by an object if it is naturally isomorphic to .

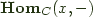We can translate that into Haskell, letting play the role of with:

(more...)

Grant B. asked me to post the derivation for the right and left Kan extension formula used in previous Kan Extension posts (1,2). For that we can turn to the definition of Kan extensions in terms of ends, but first we need to take a couple of steps back to find a way to represent (co)ends in Haskell.

(more...)

I want to spend some more time talking about Kan extensions, composition of Kan extensions, and the relationship between a monad and the monad generated by a monad.

But first, I want to take a moment to recall adjunctions and show how they relate to some standard (co)monads, before tying them back to Kan extensions.

Adjunctions 101

An adjunction between categories and consists of a pair of functors 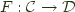, and 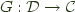and a natural isomorphism: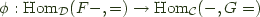

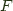We call the left adjoint functor, and 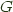the right adjoint functor and 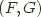an adjoint pair, and write this relationship as

(more...)

I think I may spend a post or two talking about Kan extensions.

They appear to be black magic to Haskell programmers, but as Saunders Mac Lane said in Categories for the Working Mathematician:

All concepts are Kan extensions.

So what is a Kan extension? They come in two forms: right- and left- Kan extensions.

First I'll talk about right Kan extensions, since Haskell programmers have a better intuition for them.

(more...)

 
> import Control.Arrow ((|||),(&&&),left)
> newtype Mu f = InF { outF :: f (Mu f) }
 

I want to talk about a novel recursion scheme that hasn't received a lot of attention from the Haskell community and its even more obscure dual -- which is necessarily more obscure because I believe this is the first time anyone has talked about it.

Jiri Adámek, Stefan Milius and Jiri Velebil have done a lot of work on Elgot algebras. Here I'd like to translate them into Haskell, dualize them, observe that the dual can encode primitive recursion, and provide some observations.

You can kind of think an Elgot algebra as a hylomorphism that cheats.

 
> elgot :: Functor f => (f b -> b) -> (a -> Either b (f a)) -> a -> b
> elgot phi psi = h where h = (id ||| phi . fmap h) . psi
 

(more...)